こんにちは!
講師Tです。
先日、今月2回目の中学入学準備講座を行いました。
- 分数×分数の計算
- 番外編:分数の意味と大きさ
分数同士の掛け算
前回は分数×整数の掛け算だったのですが、今回は分数同士の掛け算です。
分数の掛け算は通分や逆数になおすというような手順がなく、比較的ルールが分かりやすいので計算はできるという子が多いのではないでしょうか。
実際に計算問題を解かせてみると、どの子も問題なく計算できていました。
その中で、気になることがひとつ。
生徒の解答を見てみると、「\(\frac{1}{4}\)(4)」と書いてあります。

この分数の隣の(4)って何?

え?
よくわかんないけど、学校でそう書くって習ったから書いてる!

それって、\(\frac{4}{1}\)みたいに、分母が1になった時じゃない?

…そうだっけ?
学校の先生の方針により、「\(\frac{4}{1}\)(4)」や「\(\frac{4}{1}\)=4」と書くように習っていることは結構あります。(一般的には=の方が多数派ではないでしょうか。)
でも、問題はそこではありません。

今書いているのでいけば、\(\frac{1}{4}\)と4は同じ数って意味になってるよね

…同じ数じゃないの…?

またまたデジャブ…!?
ということで、小6範囲からは逸れますが、分数の大きさについて復習していきます。
番外編:分数の意味と大きさ
4と\(\frac{1}{4}\)の大きさ

まずは4はどんな数なのか、考えてみよう。
4は1の何個分?

4個分!

そうだね。
じゃあ、\(\frac{1}{4}\)ってどんな数だったかな?

…え?
1週間でキレイさっぱり…!
しつこいようですが、何度も同じ事を言い続け、覚えてもらうしかありません。

\(\frac{1}{4}\)は1を4等分にしたうちの1つ分って意味だったね
言葉だけで整数と分数を比べてみるのは、慣れないうちは難しいです。
そこで、数直線をかいてみます。

4と\(\frac{1}{4}\)を数直線にかいてみるとこんな感じになるよ
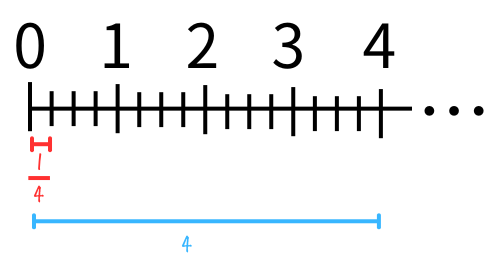

ほんとに、4と\(\frac{1}{4}\)って全然違う!
口頭でバーっと説明するだけだと、イマイチ伝わりにくいものも、図に表してみると結構すんなり理解できることも多いです。
今回は数直線を使ってみましたが、ピザやケーキの絵を使ってかいてみるのもオススメです。
分子が同じ分数の大きさ
分数の基礎部分に戻ったので、他にもいろいろな問題に挑戦してみました。
しばらくすると、手が止まっている様子。
分子同士が同じ分数の大きさについての問題です。
分子が5の真分数を大きい方ものから3つ書きましょう。
真分数とは\(\frac{2}{3}\)や\(\frac{5}{7}\)のように、分子が分母より小さい分数のことです。

分子が5の真分数だから…
\(\frac{5}{6}\)、\(\frac{5}{7}\)、\(\frac{5}{8}\)、\(\frac{5}{9}\)みたいな分数ってこと?

そうだね!
じゃあ今出た分数を大きい順に並べてみよう

1番大きいのは\(\frac{5}{9}\)!

ぶー!

え!?
9がついているため、\(\frac{5}{9}\)は1番大きそうと考える子は多いです。
こういう子には感覚的にイメージを掴んでもらうのがオススメ。
いきなり問題通りの分子で考えると難しいので、分子が1の場合で考えてみます。

\(\frac{5}{6}\)って\(\frac{1}{6}\)何個分?

5個分!

そうだね!
じゃあ、同じように考えると、
\(\frac{5}{7}\)は\(\frac{1}{7}\)の5個分、
\(\frac{5}{8}\)は\(\frac{1}{8}\)の5個分、
\(\frac{5}{9}\)は\(\frac{1}{9}\)の5個分と言えるね

\(\frac{1}{〇}\)っていうのは、1を〇等分したうちの1つ分って意味だったよね

ココで問題です!
1個のケーキを6人、7人、8人、9人で分けた時、1番大きいケーキがもらえるのは何人で分けた時でしょう。

6人!

そうだね!
同じ大きさになるように分けたとすると、6人で分けた時が1番大きくなるね

このときの1人分の大きさは1個のケーキを6等分にしたうちの1つ分だから、\(\frac{1}{6}\)と表せるよ。
じゃあ、1人分のケーキが1番小さくなるのは何人で分けた時かな?

9人!

そうだね!
同じように考えると、6人より7人、7人より8人、8人より9人というように分ける人数が大きくなると1人分は小さくなるね。

これを分数を使って、1人分の大きさを表してみると…

6人の時が\(\frac{1}{6}\)個、
7人の時が\(\frac{1}{7}\)個、
8人の時が\(\frac{1}{8}\)個、
9人の時が\(\frac{1}{9}\)個!

そうだね!
じゃあ、この中で大きい順に並べていくと…

\(\frac{1}{6}\)、\(\frac{1}{7}\)、\(\frac{1}{8}\)、\(\frac{1}{9}\)の順になる!

正解!
問題では分子が5の時について考えるけど、今使った分数のそれぞれ5個分の大きさを考えてみてね。
大きさの順番が分かったら、あとは大きい方から3つ書いてみよう!
分子が同じ分数は「分母が大きいほど数は小さくなる」と習うこともあります。
しかし、細かい場合分けをしていくとなかなか覚えられなくなってしまいますよね。
特に分数の大きさ比べは整数の時と感覚が違うので混乱する子が多いです。
通分して大きさを比べるという手もありますが、このあたりが苦手な子たちにとっては通分も難しいはず。
そんな時は分数そのものの意味から考えると、覚えることも少なく、楽に考えられるのでオススメです。
ふりかえり
今回は分数の計算を中心に扱う予定だったのですが、かなりさかのぼったところまで話をすることとなりました。
算数が苦手な子たちにとっては、「分かったかも!」→「あれ?どうするんだっけ?」→「分かったかも!」の繰り返しが1番効果的だと思います。
今回の話も度々していますが、時間が空くとまっさらになっているのはよくあることです。
大事なのは分からなくなったときに、その分からないを無視しないこと。
何回でも同じもので立ち止まって考えていくうちに身についていきます。
さて、次回の講座は3月20日に行います。
次回も分数やその計算を扱っていく予定です。
受講者まだまだ募集中ですので、お気軽にお申込み・お問合せくださいね^^
中学入学準備講座のご受講のお申込み・お問合せはコチラ↓
学習塾クローネのLINE公式アカウントでは毎月1ヶ月ごとに人気ブログ記事をご紹介しています。
友だち追加で人気記事をお見逃しなく!![]()



