2025年5月号　今月の挑戦問題の解説

今回はクローネ通信（塾通信）2025年4月号に掲載した問題の解説です。

今月の問題は4月に実施した小学生の模試で出題されたものから類題を作成しています。

中学受験者ではなく、三筑中学校や板付中学校などの地元公立中学へ進学予定の子を対象とした模試です。

2025年5月号　1問目　小4の模試から類題

少し長いので、4枚入りの袋をA、6枚入りの袋をBと表記していきます。

解き方①：コツコツ探す

問題の指示に従い、「1袋4枚入りのクッキーをできるだけ少なく買う」「合計44枚買う」という条件をもとに考えてみます。

44枚ぴったり買わないと！と考えてしまうと難しくなるので、この段階では合計44枚前後になるようにというように合計枚数についてはゆるめの設定でOKです。

では、早速、買うクッキーの袋のうち、Aが1番少なくなる「0個」と設定して考えてみましょう。

（Aの数）　Aのクッキーの数	(Bの数)　Bのクッキーの数	クッキーの合計枚数
(0)　0	(7)　42	42

Bの6枚入りの袋だけを買うとすると、44枚には足りないようです。
（Bの数を8個とし、48枚買うと考えてもOK。この場合も44枚ぴったりにはなりませんね。）

では、Aの数を、2番目に少ない数「1個」に設定して考えてみます。

（Aの数）　Aのクッキーの数	(Bの数)　Bのクッキーの数	クッキーの合計枚数
(0)　0	(7)　42	42
(1)　4	(6)　36	40

クッキーの合計枚数を見てみると、40枚。
44枚と比べると4枚分の差です。

（Aの数）　Aのクッキーの数	(Bの数)　Bのクッキーの数	クッキーの合計枚数
(0)　0	(7)　42	42
(1)　4	(6)　36	40
(2)　8	(6)　36	44

クッキーの合計枚数が44枚ぴったりになりました！

このように条件を手がかりにし、コツコツ探し出す方法があります。

解き方②：置き換える

Aの袋にはクッキーが4枚、Bの袋にはクッキーが6枚入っていました。

クッキーの合計枚数が44枚となるAとBの袋の数について、その組み合わせを考えてみましょう。
（この段階では「Aをできるだけ少なく買う」という条件は一旦無視して考えてOKです。）

今回はAを11袋、Bを0袋の組み合わせを使って考えていきます。

Aを11袋買い、それだけで44枚クッキーを買うとすると、このような図ができます。

今回は「Aをできるだけ少なく買う」という条件があるので、ここからAの数を減らしていきたいと思います。

ここで使うのが「置き換え」です。

4と6の最小公倍数は12なので、Aが3袋、Bが2袋の時、それぞれのクッキーの枚数は同じになります。

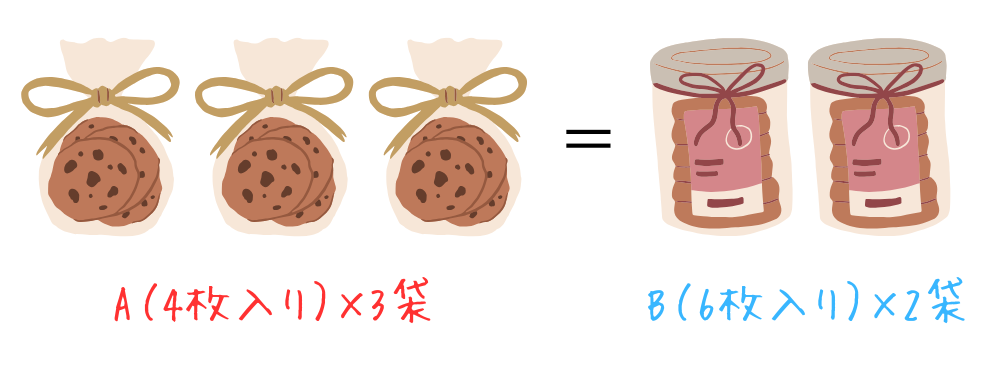
Aが3袋あれば、Bの2袋分と同じクッキーの枚数になるので、Aの袋3つごとにBの袋2つ分に置き換えてみます。

できるだけAが少なくなる、逆に言うとBを多く買うようにするとこのように置き換えることができます。

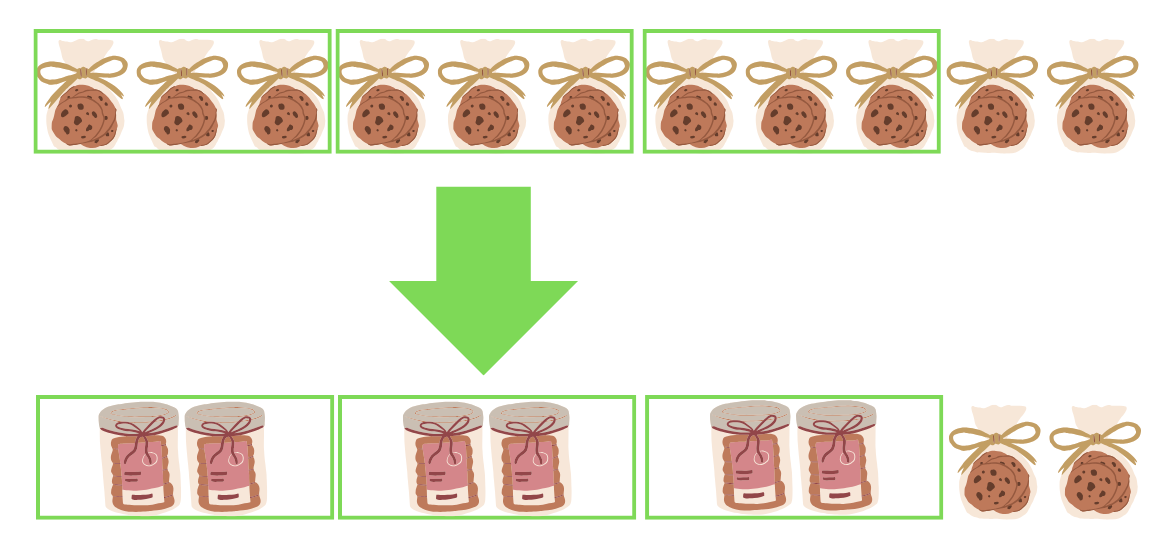
Aが2袋、Bが6袋となり、これ以上置き換えることができないので、この組み合わせの時、問題文の条件を満たすこととなります。

2025年5月号　2問目　小5の模試から類題

解き方

「プリントシュークリームの個数の合計ができるだけ多くなるように」とあるので、150円のシュークリームをできるだけたくさん買ったとき、この条件を満たせることになります。

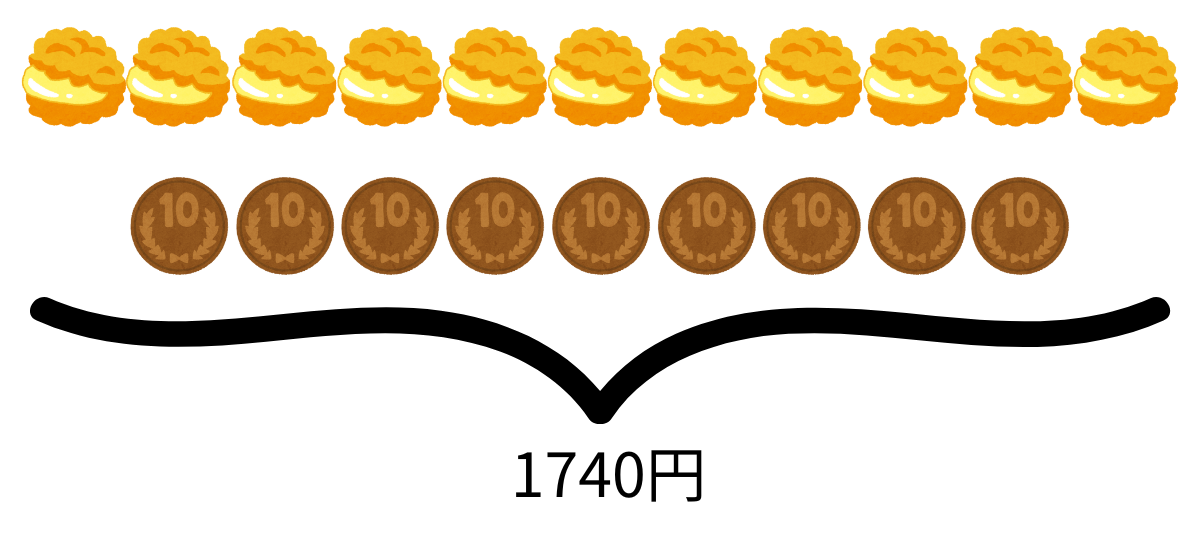
1740円を超えない範囲で、150円のシュークリームをできるだけたくさん買うとき、
1740÷150＝11あまり90
よって、シュークリームは11個買うことができます。

次に、プリンとシュークリームの値段の差を考えてみましょう。

プリンは1個180円、シュークリームは1個150円なので、その差は30円。

言い換えると、シュークリーム1個＋30円でプリンが1つ買えることになります。

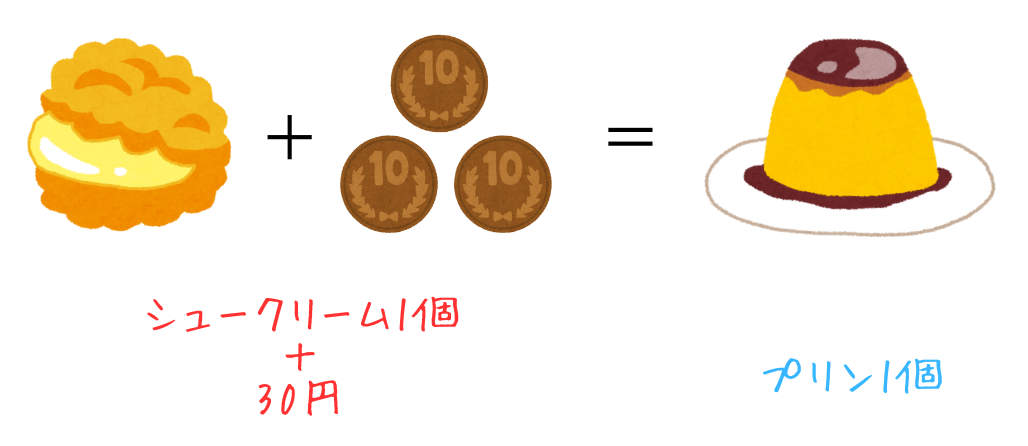
プリンもできるだけ多く買いたいので、シュークリーム1個と30円の組み合わせをプリン1個に置き換えてみます。

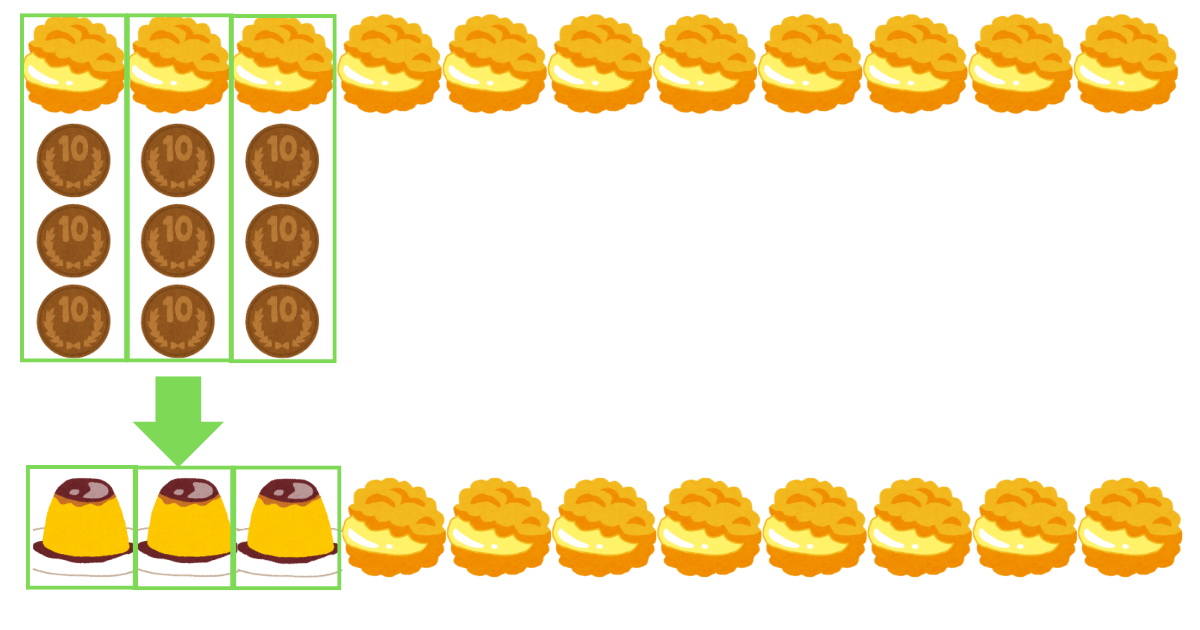
以上より、プリン3個、シュークリーム8個の時問題文の条件を満たすので、これが答えとなります。