今回はクローネ通信(塾通信)2025年3月号に掲載した問題の解説です。
2025年3月号 1問目
あるクラスの人数は32人で、女子は男子より4人多いです。
このクラスの女子の人数は何人ですか。
線分図を使って考える
線分図という図を使って考えると小学生でも解きやすいです。
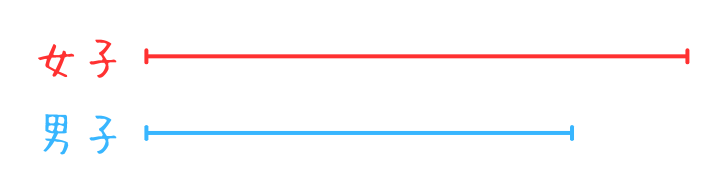
男子の人数を表すものと女子の人数を表すものの2本の線分図を用意します。
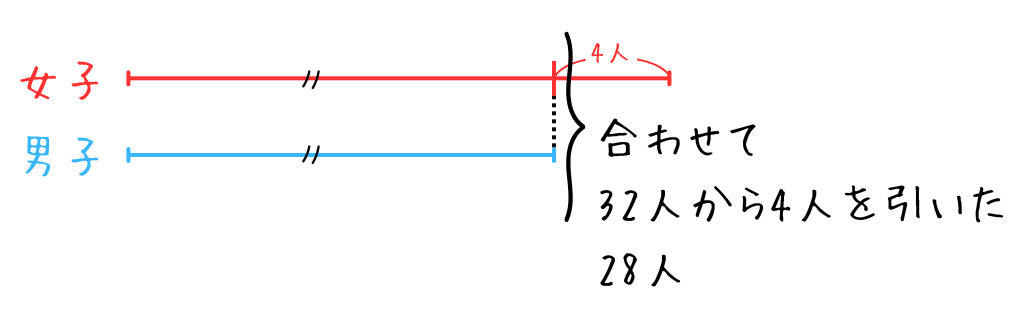
「女子は男子より4人多い」とあるので、女子の方の線分図に男子より多い4人分をかいておきます。

女子-4人分の長さは男子の長さと同じ。
また、女子-4人分と男子の人数を合わせた数は28人となります。
28人のうち、半分は男子なので男子の数は14人。
女子は男子より4人多いので18人となります。
一次方程式で解く
中1で学習する一次方程式を使って解くこともできます。
女子の人数を\(x\)人とすると、男子の人数は\((x-4)\)人と表せます。
女子+男子=クラスの人数になるので、
\(x+(x-4)=32\)
という方程式がたちます。
これを解くと、\(x=18\)
女子は18人と求めることができます。
2025年3月号 2問目
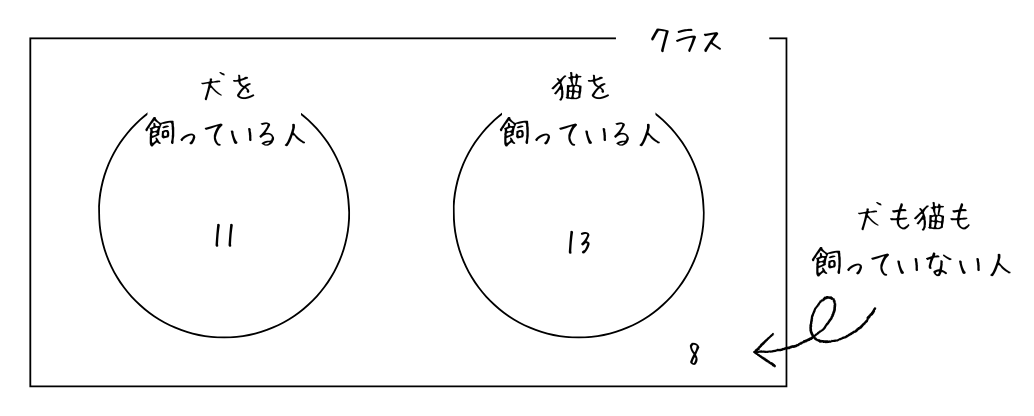
あるクラスの人数は30人で、犬を飼っている人は11人で猫を飼っている人は13人です。
また、犬も猫も飼っていない人は8人です。
犬と猫の両方を飼っている人は何人ですか。
ベン図を使って考える
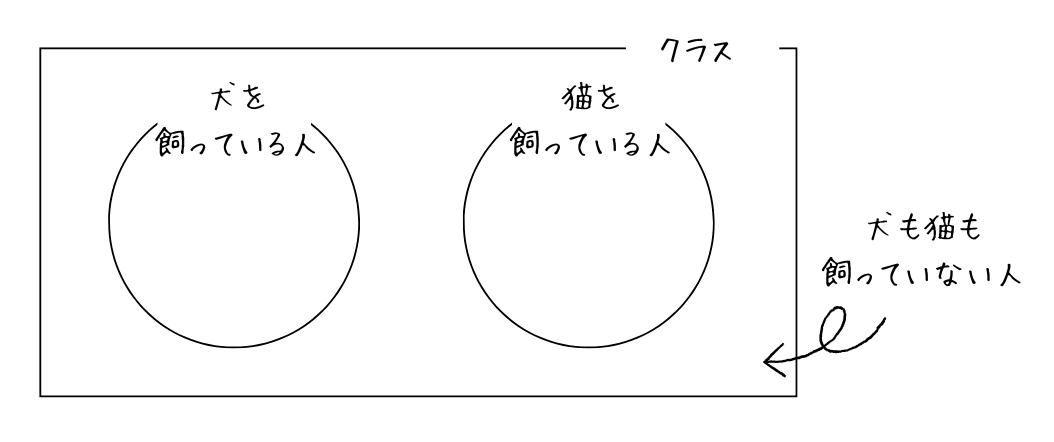
ベン図とはこんな図のこと。
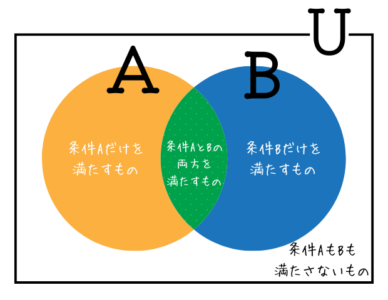
正式に学習するのは高校生になってからなのですが、小学校や中学校の教科書にさりげなく登場していることもあるので、高校生になるまで見たことない!という子は少ないかと思います。
では、早速解いていきましょう。
今回の問題では犬と猫の両方を飼っている人の人数が分からないので、まずは犬を飼っている人と猫を飼っている人とそれ以外の人の3つに分けて考えてみます。
先程の例の集合Aを犬を飼っている人の集合、集合Bを猫を飼っている人の集合として書いてみました。
具体的に図に問題文の条件を書き込んでいくとこんな感じです。
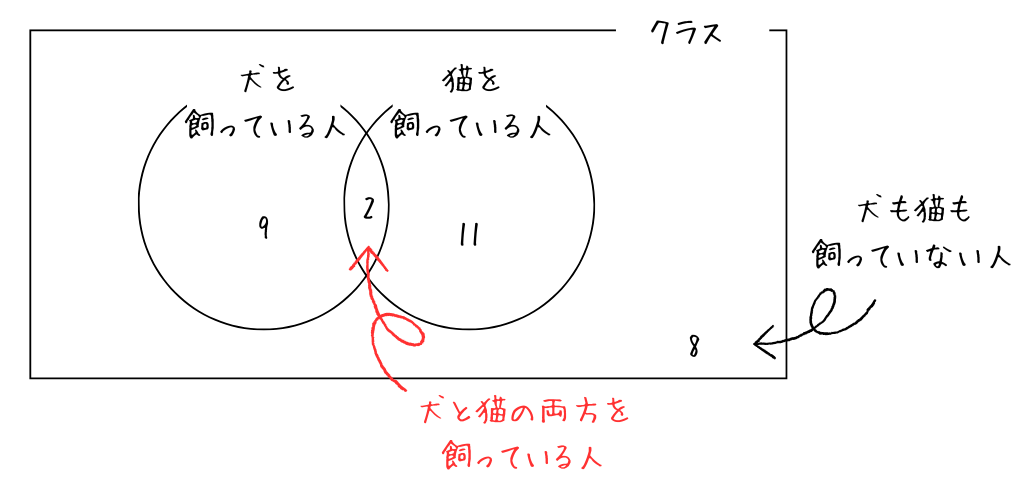
しかし、今書いた数を足すと32人で、これは合計人数より多くなってしまいます。
ここで考えるのが両方飼っている人の人数です。
今書いた図では、両方飼っている人の数を犬を飼っている人として1回、猫を飼っている人として1回の合計2回数えていることになります。
余計に数えた分が、合計の人数30人より多くなっている分なので、両方飼っている人の人数は2人と分かります。
表を使って考える
小学校ではこんな表を使う考え方が多いかもしれません。
| 犬\猫 | 飼っている | 飼っていない | 合計 |
| 飼っている | |||
| 飼っていない | |||
| 合計 |
それでは、問題から分かる数を埋めていきます。

新しく書いたところは赤文字で書いています
| 犬\猫 | 飼っている | 飼っていない | 合計 |
| 飼っている | 11 | ||
| 飼っていない | 8 | ||
| 合計 | 13 | 30 |
今書いた数字から、さらに分かるところを埋めていきます。
犬を飼っていない人の合計と猫を飼っていない人の合計が出せます。
| 犬\猫 | 飼っている | 飼っていない | 合計 |
| 飼っている | 11 | ||
| 飼っていない | 8 | 19 | |
| 合計 | 13 | 17 | 30 |
今度は犬を飼っているが猫を飼っていない人、犬を飼っていないが猫を飼っている人の人数が分かりそうです。
| 犬\猫 | 飼っている | 飼っていない | 合計 |
| 飼っている | 9 | 11 | |
| 飼っていない | 11 | 8 | 19 |
| 合計 | 13 | 17 | 30 |
ここまでできたら、最後に犬と猫の両方を飼っている人の人数を出してみましょう。
| 犬\猫 | 飼っている | 飼っていない | 合計 |
| 飼っている | 2 | 9 | 11 |
| 飼っていない | 11 | 8 | 19 |
| 合計 | 13 | 17 | 30 |
このように、表を使うとわかるところから埋めていくうちに答えが出せます。